一般的商品搾取定理(Generalized Commodity Exploitation Theorem)について
(下の方に06年9月15日の追記を挿入しています。9月19日修正。10月8日修正。08年7月24日修正。09年7月1日修正。)
一般的商品搾取定理(一般化された商品搾取定理とも訳す)について
一般的商品搾取定理は経済理論学界の雑誌でも批判したし、もともとバカバカしいから賛同者もあまりいないだろうと思っていたら、いつのまにやら「マルクスの基本定理」はこれによって否定されたという見方が定着してしまったような感じがある。
そこでここで、一般的商品搾取定理によるマルクスの基本定理批判が成り立たないことを、アマチュアにもわかりやすいにように徹底的に説明したい。
マルクスの基本定理は、正の利潤の存在と労働の搾取の同値性を示したものと言われるが、正確には労働の搾取だけでなくて「純生産が可能」という条件を前提している。つまり、
純生産可能+労働の搾取 ⇔ 正の利潤の存在というふうになっているのである。純生産が可能という条件は当然の前提とみなされるので、省略されているのである。
「純生産」可能+バナナの搾取 ⇔ 正の利潤の存在ところがマルクスの基本定理が労働の搾取の背後に前提している純生産可能条件と、このときの「純生産」可能条件は違う。前者はごく当たり前の純生産が可能になることであり、自明視して省略してもかまわないが、後者は極めて奇妙な「純生産」について言われている条件であり、それは必ずしも自明ではない。実は労働者への分配の制約を含意している社会的条件なのである。
このことを示すために、まず、マルクスの基本定理を改めて証明する。別のページに示したわかりやすい証明ではなく、正攻法で正面突破するので、覚悟してついてきてほしい。
Aをn部門投入係数行列、τをn部門直接労働投入係数ベクトル(横)、bをn部門実質賃金率ベクトル(縦)とする。Aに、n+1行としてτを、n+1列としてbを追加した行列をA+とする。すなわちこれは、労働部門を第n+1部門としたときの投入係数行列である。すなわち、
このとき、正の利潤の存在は次のように表される。
∃p>0, p(I−A+)>0このことの必要十分条件は、I−A+がホーキンズ・サイモン条件を満たすことである。それは、I−A+の主座小行列式(首座? どっちだろう?)がすべて正ということである。k次の主座小行列式とは、左上隅から順にk行k列をとってつくった正方行列の行列式のことで、今の場合、ホーキンズ・サイモン条件が要請するのは、左隅の第1行第1列要素である1次の主座小行列式から、行列全体の行列式であるn+1次の主座小行列式まで、これらがすべて正ということである。すなわち、
ただし、Iの添字は単位行列の次元を表すが、以下では自明なので略す。(当初、上記二次の首座小行列式の2行2列のaの添字が12となっていたが、もちろん22の誤記だったので修正した。横田静夫氏のご指摘により改めた。2014年8月1日)
for any y>0, ∃x>0, (I−A)x=y (1)*)すなわちこれは、xをn次元の総生産ベクトル(縦)と見ると、「純生産が可能」ということを表している。
一番下の直接労働投入係数ベクトルを、余因子計算で抜いた行にそれぞれもっていくと、行を一回入れ替えるごとに正負が入れ替わるので、最後の項(I−Aの行列式)以外の項は全部マイナスになる。
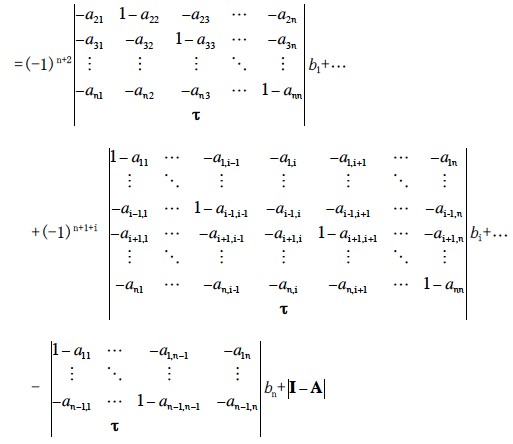
(08年7月24日式の表記ミス修正)
すなわち、さっきのbiにかかっている係数というのは、tiにI−Aの行列式をかけたものだったのだ。したがって、I−A+の行列式が正というのは、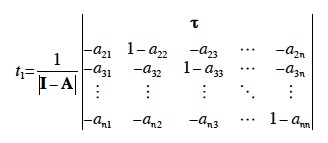
…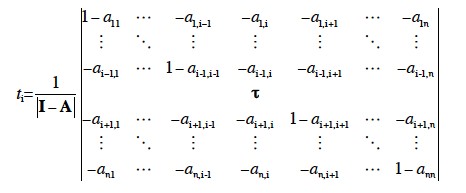
…
ということである。純生産可能条件から、I−Aの行列式は正だったから、このことは1−tbが正ということを意味する。これが労働の搾取である。
さて、これと同様の手続きで、一般的商品搾取定理を見てみることにしよう。事態の本質はI−A+がホーキンズ・サイモン条件を満たすという条件であり、全く変わらない。問題はこれをどう分けるかである。
今、バナナでも鉄でもいいのだが、第n財を投下価値財として、I−A+の第n+1行、第n+1列に持っていき、今まで第n+1行、第n+1列にあった労働力部門を第n行、第n列に持っていくことにする。ナンバリングを変えただけだから、本質的には何も変わらない。
ここで、Aから第n財を除き、第1財から第n-1財までで構成したn-1次元の投入係数行列をA−とし、これに第n行として直接労働投入係数ベクトル(第n要素を除く)を、第n列として実質賃金率ベクトル(第n要素を除く)を追加した行列をA*と表記しよう。
利潤の存在は先ほどと同じ、
∃p>0, p(I−A+)>0で表される。したがって、このための必要十分条件も先ほどと同じ、I−A+の主座小行列式がすべて正ということである。
for any y*>0, ∃x*>0, (I−A*)x*=y* (2)これは、先ほどの労働搾取ケースの(1)式にあたるものだが、(1)式の場合の純生産y≡(I−A)xと、今回の(2)式の「純生産」y*≡(I−A*)x*とは、いったいどう違うのだろうか。Aの第n行から第n要素を除いたn-1次元横ベクトルをan、Aの第n列から第n要素を除いたn-1次元縦ベクトルをanとする。また、xの第n要素を除いたn-1次元縦ベクトルをx−、yの第n要素を除いたn-1次元縦ベクトルをy−、bの第n要素を除いたn-1次元縦ベクトルをb−、τの第n要素を除いたn-1次元縦ベクトルをτ−とする。また、総労働量をLとする。すると、
よって、通常の純生産概念には含まれるはずの労働者の取得する財bLがこの場合の「純生産」には含まれておらず、通常の純生産概念には含まれていない第n財生産のための諸財の投入anxnがこの場合の「純生産」に含まれている。第n財の純生産そのもの、xn−(anx−+annxn)は、この場合の「純生産」には含まれていない。,
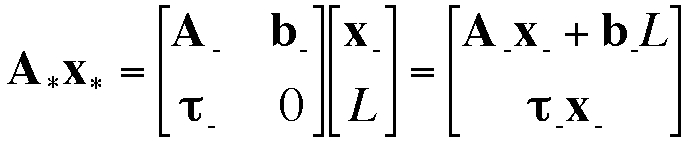
∴ y−*− y−=A−x−+anxn−A−x−−b−L=anxn−b−L
1−t−b−>0ただし、t−は第n財の投入を無視したときの直接間接投下労働量であり、
t−(I−A−)=τ− (3)で定義される。tb>t−b−だから、この条件は労働の搾取よりも緩い。しかし何らかの社会的な分配条件には違いない。
追記:このかん、吉原直毅さんとのやりとりで次のことが明らかになっています。(a) 利潤の存在⇒(労働も含む)すべての商品の搾取(a)は吉原さんが示したものです。(a)は簡単確実に言えます。利潤が存在すれば、すべての商品の搾取が成り立つだけでなく、もちろんその背後にはあらゆる意味での「純生産」可能条件が成り立っています。
(d) (通常の)純生産可能条件と労働以外のある特定商品の搾取を満たしても、利潤が存在しないことはあり得る。(d)は、私の主張で、I−Aのホーキンズ・サイモン条件が満たされて、第n財の搾取が存在しても、I−A*がホーキンズ・サイモン条件を満たさないために利潤が正でなくなるケースがあるということです。当然この時には、労働の搾取もないわけです。自然な純生産可能条件であるI−Aのホーキンズ・サイモン条件と単独で組み合わさって利潤の存在が言える商品搾取は労働の搾取だけで、他の商品搾取はI−Aのホーキンズ・サイモン条件と単独で組み合わさってもそれだけでは利潤の存在を導けないということです。
私はこれを示すために次のような数値例を作りました。I−A*がホーキンズ・サイモン条件を満たさないならば、投下第n財価値ベクトルの正値性は満たされません。上の数値例でも、ν2<0となっています。
一番簡単に、置塩『蓄積論』の二部門モデルでやります。
第1部門が生産手段で、第2部門が消費財、aiが第i財を1単位生産するために必要な生産手段の投入量、τiが第i財を1単位生産するために必要な労働の投入量、実質賃金率を消費財b単位とします。
投下労働価値tiは次のように定義されます。
t1=t1a1+τ1
t2=t1a2+τ2
これを解くと、t2=a2τ1/(1-a1)+τ2 となります。
投下第1財価値νiは、次のように定義されます。(ギリシャ文字のニュー)
ν2=ν3τ2+a2
ν3=ν2b
これを解くと、ν3=a2b/(1-τ2b) となります。
すると、単位労働力の労働価値μ3は、
μ3=t2b
となります。単位第1財「力」の投下第1財価値μ1は、
μ1=ν3τ1+a1=a2τ1b/(1-τ2b)+a1
となります。
ここで、純生産可能を満たし、第1財搾取がプラスで、しかし労働搾取がマイナスなのでしたがって利潤が負になる例を示しましょう。
a1=0.5, a2=0.2, τ1=1, τ2=2 で、b=1とします。
a1=0.5<1 よって、純生産可能条件を満たす。
μ1=0.2/(1-2)+0.5=-0.2+0.5=0.3<1 よって第1財搾取はプラス。
t2=0.2/0.5+2=2.4
μ3=t2b=2.4>1 よって、労働搾取はマイナス。
なお、一般的商品搾取定理そのものについての議論は上で終わっており、以下は誤解をさけるための付け足しの話です。
吉原さんにはやりとりに積極的におつきあいいただき、深く感謝しています。
(※ 以上、2006年9月15日追記。翌日吉原さんから、(b)と(c)に前提していた「Aの分解不能性」という前提をはずした証明を受け取ったので、9月19日にその点についての記述を修正。)
(※ 当初、(b) ある自然な前提のもとで「労働の搾取⇒純生産可能条件」、(c) 「(労働も含む)すべての商品の搾取⇒純生産可能条件」という二つの命題が含まれていた。(b)は吉原さんが証明したもので、私も一応フォローした。しかし、その後吉原さんが一般的条件のもとではここにおける前提は経済学的に自然とは言いがたいと結論している。(c)は吉原さんが証明を試み、私も成り立つことを予想していたものである。しかし、その後吉原さんは証明を断念し、それと独立に私が反例を発見し、これが成り立たないことを合意した。2006年10月8日)
なお、一般的商品搾取定理は、よく「石油1リットル掘り出すのに直接間接に1リットル以上石油が必要ならば利潤が出ない」というふうに説明される。この説明自体は間違いではないのだが、この場合の「間接」には、労働を経由したものも含まれることに注意されたい。石油を掘り出すために働く労働者が石油を直接間接に消費しているものまで含めるのである。ところがこの説明だけ聞くと、あたかも労働のことを考えない技術的な条件のように聞こえてしまい、それももっともだと思ってしまう。もしこれが労働のことを考えない技術的条件ならば、石油1リットル掘り出すのに直接間接に必要な石油が1リットルに満たなかったとしても、それだけでは利潤は出ない。それは、純生産可能条件の一部を成す自明の条件にすぎない。
第n財の技術的な直接的間接的投入量で各財を評価するベクトルをvとすると、(3)式と同様にそれは次のように定式化される。
v(I−A−)=anしたがって、上記の議論がそのままあてはまり、I−Aの行列式は、I−A−の行列式と、1−van−annの積になる**)。よって、利潤の存在のためのI−A+の行列式が正という条件の方は以下のように変形される。
|I−A−|(1−van−ann)(1−tb)>0すなわち、石油1リットル掘り出すのに直接間接に必要な石油が1リットルに満たないということが、技術的な条件として言われていること(1−van−ann>0)ならば、利潤が正になるためには別途労働の搾取(1−tb>0)が必要なのである。
2006年8月31日作成
∃x>0, for any y>0, (I−A)x=y (1)となっていたが、これは、あらゆるy>0を単独で生み出せるスーパーx>0が存在するという意味になるので、ミスである。吉原直毅氏の指摘にしたがって改めた。細かい式表現までフォローしていただいて感謝している。(2006年9月15日)