松尾匡のページ
09年3月19日 犯罪と失業 REVISED!!
筑摩書房のウェブ雑誌、「webちくま」の連載を依頼されたんだが、これが何回書き直しても原稿がボツになるのを繰り返した。
いや別に不満を述べているわけではない。自分ではわかりやすい文章を書けるつもりだったが、それがひとりよがりだったことが思い知らされて、いい修行になっていると真面目に思う。
「景気について」というのがお題なのだが、僕のアイデアは、「グラフなどで使うデータはウェブでダウンロードできるものに限る、そしてすべてリンクをつけて誰でも分析を再現できるものにする」というものだった。だから、本当はデータを加工して使った方がいいものも、読者の手軽さのために、あえて目をつぶってなるべく加工しない──なんてやさしい読者サービス、とうぬぼれていた。てゆーかまあ、授業用教材として課題に使いたいって魂胆もあったんだけど。
ところがこんな発想自体、出版社側からすれば困りものだったみたい。わざわざデータをダウンロードしてみようなんていう読者がどれくらいいるか、かえって煩雑になって読者を失うって心配されたらしい。僕の考える読者サービスってのは、「難しい分析はやめて回帰分析ぐらいにとどめたいけど、それでも難しく思われるかもしれないから、それもあえてやめておこう」ってレベルのものだった。でももし自分で回帰分析した読者が出たときのために、「誤差の系列相関」とか出ますからそのまま使えませんよってちょっと書いておこうとか、そんな気遣いをしていた。そしたら、「回帰分析」って言葉も、「誤差の系列相関」って言葉も、そもそも統計学用語は禁止って通達がきた。うーむ。
証拠や参照のためにリンクをつけたところもあったのだけど、これも、コンパクトにズバリ目的の文章が把握できない限り、読者が煩わしいからやめろということになった。うーむ。
データをなるべく加工していないことの言い訳の文章自体やめてくれと言われたし、うーむ。
結局折れ線グラフを見せるだけになるので、「似た動きをしている」ぐらいしか言えないと思うけど、逆に話を膨らませろというお達し。うーむ。
ようやくなんとか認められたみたいだけど、このままでは、ウェブ掲示板とかで「バーカ、バーカ、頭悪すぎ」とか書かれそうで怖い。そりゃ実際周知のことだから今さら書かれたってかまわないはずなんだけど。
まあ、第1回めは、例の「犯罪と失業」の話から始めるので、ここでとりあえずこれまでの研究の結果を紹介して、あり得べき読者の批判に備えておこう。掲示板で「頭悪すぎ」とか書いてあるのを見たら、このページを教えてあげて下さい。まあかえって叩くネタを増やすようなものかもしれないが。
以下、ウェブ雑誌の読者の中に、実際にやってみようと思う人がいらっしゃったことも想定において書くので、専門家にとっては煩わしい説明も多いと思うがご容赦を。私も計量経済学の専門ではないので、何か間違ったことを書いてしまっていたら、是非ご指摘下さい。
【経緯】
一年あまり前、久留米大学の三年生のゼミ生が、犯罪発生件数と過去数年の失業率の平均との関係を回帰分析したところ、非常に良好な実証結果が出たように思われたので、このサイトで記事に取り上げた。
「犯罪の九割は失業率で説明がつく」
そしたら、これが「はてなブックマーク」で500以上集めたり、いろいろなブログで取り上げられたりして、思わぬ注目を集めた。その中で、この分析結果には、「誤差の系列相関」と呼ばれる問題(後述)があることが明らかになり、その点の改善に取り組んだ結果が、次の続報である。
「やっぱり九割がたの説明がつく──犯罪と失業率続報」
とりあえずこの段階での結論では、犯罪率を前年の犯罪率とその年の失業率で回帰させたものが、非常に良好な実証結果になって、当初の「誤差の系列相関」の問題もクリアできていた。
まあ、ウェブ雑誌の原稿では、「煩雑」ということで、この二件へのリンクも本文中では禁止されてしまったけど。
この「続報」記事の書き出しの部分では、津島昌寛氏の年齢別に分けた先行研究はじめ、拙記事に触発された、国別とか犯罪種別とかの研究記事をリンクしたのでご参照いただきたい。また、このあと、id:eliya氏による、県別データを使った犯罪率と失業率の相関を分析した結果が報告されている。
「失業率と犯罪の関係:県別データを用いた分析(その一)」
「失業率と犯罪の関係:県別データを用いた分析(その二)」
上のものは、2000年から2006年までのデータを使うと有意な正の相関が実証されたというもの。あとのものは、単年の県別データでクロスセクション分析すると、相関係数は年々低下して2006年では有意でなくなるというもの。この後者の結論は理由が不明であるが非常に興味深い。
ところでその後、警察大学校警察政策研究センターの鈴木定光教授が、『警察學論集』第61巻第8号(2008年8月)に、「犯罪はなぜ変化するか──統計からみたその動向」という論文を載せている。ここで、鈴木氏は、犯罪種類を細かく分けて、それぞれ経済指標との相関を調べている。相関分析に使っているのが平成9年からの10年間の年次データだけで、しかも相関係数しか見ていないなど、統計分析としては不十分なものであるが、専門の犯罪学者の知見で説明を補っている。
それによれば、空き巣、出店荒し、自動車盗、車上ねらいは失業率と非常に高い正の相関を示し、事務所荒し、置き引き、強盗はやや高い正の相関を示した。また、万引き、暴行、傷害、公務執行妨害は、勤労者世帯実収入と高い負の相関を示したと言う。
もっとも、暴行と公務執行妨害については、他の犯罪種と違って、景気回復した近年でも増え続けている。だから、基本的に低下傾向が続いた勤労者世帯収入との間に相関があるような見かけがでるのは当然とも言える。
【犯罪と失業再び】
さて今回、ウェブ雑誌で取り上げるに当たって、もう一度犯罪と失業の関係を確認してみることにする。以下では、データは次のものを使う。
犯罪認知件数(1953-2004):総務省統計局のサイトの「日本の長期統計系列」第28章より
http://www.stat.go.jp/data/chouki/zuhyou/28-01.xls E列「一般刑法犯認知件数」
犯罪認知件数(2005-07):警察庁のサイトの「平成19年の犯罪」より
http://www.npa.go.jp/toukei/keiji36/Excel/H19_003.xls C列
完全失業率(1953-2007):総務省統計局サイトの「労働力調査 長期時系列データ」「参考表2」
http://www.stat.go.jp/data/roudou/longtime/zuhyou/lt02.xls I列
(但し、1973年は沖縄県を含むもの。*のついているデータは沖縄県を含まない。)
人口(1953-2006):総務省統計局のサイトの「日本の長期統計系列」第2章より
http://www.stat.go.jp/data/chouki/zuhyou/02-01.xls C列
人口(2007):政府統計の総合窓口「人口推計」より
http://www.e-stat.go.jp/SG1/estat/Xlsdl.do?sinfid=000002237389 D21セル
一般刑法犯認知件数を人口で割った、人口千人あたりの一般刑法犯認知件数を、以下で「犯罪率」と呼ぼう。犯罪率と失業率の推移をグラフにすると、上記拙記事であげた下のようになる。この先2007年までのデータは、失業率、犯罪率ともに低下を続けている。
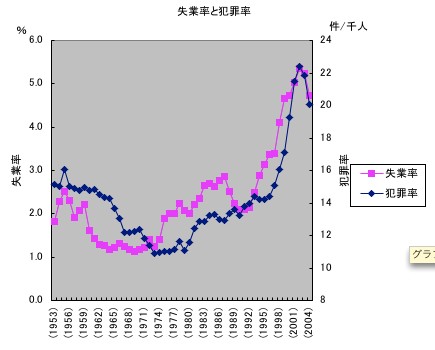
さて、まず両者の単純回帰を見たいのだが、グラフを見ると、近年の失業率が高い状態では、失業率が低い頃と比べて、犯罪率の増減の反応が早いことが見て取れる。つまり、横軸に失業率、縦軸に犯罪率をとってグラフにすると、右上がりというだけでなくて、失業率が高くなればなるほど、犯罪率の上がり方が増大するという、右下に向かって凸の曲線になっている。
したがって、一次式の直線で回帰するためには、グラフが右上に行ったときの伸び方を押さえるため、犯罪率はlogをとっておいた方がいい。(以下では自然対数。エクセルではLN)
そうすると、単純な回帰分析の結果は次のようになった。
[回帰式A] 期間1953-2007、標本数55
log 犯罪率=9.609+1.855×失業率
重決定係数0.659、定数項のp値2.78×10-25、失業率の係数のp値5.46×10-14、ダービン・ワトソン値0.186。
残念ながらダービン・ワトソン値が低すぎて、誤差が系列相関していることがわかった。
「誤差の系列相関」というのは何かと言うと、本当の説明変数(今の場合log 犯罪率)と、回帰式から計算される説明変数の予測値(今の場合9.609+1.855×失業率)との間のズレが、本当なら毎年毎年デタラメの無関係になっていなければならないのに、過去のズレの影響を受けてしまっているということである。そうすると、回帰分析は正確にできなくなってしまう。上記分析結果は、p値、すなわち、本当はゼロなのに偶然そんなふうな値に計測されてしまった確率が、ほとんどゼロに近いので、ほぼ確実にこんな関係が言えるという、とても望ましい結果が出ているのだが、誤差の系列相関がある以上は、いくらいい結果に見えても信頼できない。
これは、ダービン・ワトソン値を見ればわかる。これが2に近ければ系列相関がないと言える。0.186では低すぎて明らかにプラスの系列相関がある。つまり、説明変数の実測値と予測値とのズレが去年大きかったならば、今年のズレもそれにひきずられて大きくなる。エクセルで回帰分析したときには、「残差」を表示する設定にすればそれを見ることができるが、プラスの値とマイナスの値がそれぞれかたまって出てくるので、いかにも過去の残差の影響を受けていることがわかる。(「誤差」と言ったり「残差」と言ったりいろいろ出てくるが全部同じこと。被説明変数の実測値と回帰式から計算される予測値との間の差のことである。)
ダービン・ワトソン値はエクセルでは自動的には出ないのだが、SUMXMY2(残差の二番目から最後まで,残差の最初から最後の一つ前まで)をSUMSQ(残差全体)で割れば出る。
【2SPW法】
では誤差の系列相関があるときはどうすればいいのか。私が大学院の頃習ったのは「コクレン・オーカット法」と言って繰り返し収束計算を使うものだった。去年は上記「続報」記事にあるように、これをエクセルで手計算する「アルゴリズム体操」に挑戦して大変な目にあったのだが、その後、蓑谷千凰彦『計量経済学』(多賀出版)を勉強してみたら、コクレン・オーカット法はダメだと書いてある。その代わりに勧めているのが、「2ステップ・プレイス・ウインステン(2SPW)」である(p. 181-)。読んでみたら収束計算とかしなくていいじゃないか。一発で出る。去年のあの苦労は何だったんだ。
「誤差の系列相関」が、次のようなものだと考えよう。
今期の残差=ρ×前期の残差+本当に出鱈目な誤差
そうすると、「今期の残差−ρ×前期の残差」が誤差項になるように、うまいこと変数を変換してやれば、普通の回帰分析を使えることになる。ただし、第1期目は、「√(1−ρ2)×第1期目の残差」が誤差項になるようにする。
そうすると、変数変換も同様に、「今期の変数−ρ×前期の変数」としてやればよい。第1期目も同じく「√(1−ρ2)×第1期目の変数」としてやる。定数項に関しては、第1期目が√(1−ρ2)で、2期目以降1−ρとなるダミー変数みたいなもの(以下Cと書く)を作ってやる。
そして、
変換後の被説明変数=α×C+β×変換後の説明変数
を、「定数に0を使用」で回帰分析してやればよい。
ただし、ρは未知なので、代理の推測値を使う。三種類ほど流儀があるらしいのだが、ここでは、「ユール・ウォーカー方程式」とかいうものから出てくるらしいものを使う。エクセルの式では、SUMPRODUCT(残差の二番目から最後まで,残差の最初から最後の一つ前まで)をSUMSQ(残差全体)で割れば出る。このやり方を選んだのは、あとで、「h統計量」というものを計算するのだが、そのときに使うρがこれと同じものだからだ。
さて、それで、変数変換したのを回帰分析したら、このようになった。ρ=0.879だった。
[回帰式B] 期間1953-2007、標本数55
log 犯罪率を変換した変数=10.498×C+1.515×失業率を変換した変数
重決定係数0.902、Cの係数のp値9.67×10-14、失業率を変換した変数の係数のp値1.30×10-5、ダービン・ワトソン値1.034。
上述の単純な結果よりも決定係数はいい。それでもやはり、ダービン・ワトソン値はまだ足りない。判定の表は蓑谷さんの本の498ページあたりに載っているのだが、ここの標本数55のところの、dLの値よりも小さければ、ρ=0(系列相関なし)という仮説は1%水準で棄却されてしまう。実は私は、この2SPW法のような場合、変数の数が1個を見ればいいのか2個を見ればいいのかわからないのだが、変数の数が1のときのdL=1.356、2のときのdL=1.320と、いずれにしても今出た1.034では小さすぎてダメである。
【前年の犯罪率とその年の失業率で回帰】
そこで今度は、去年成績がよかった、犯罪率を前年の犯罪率とその年の失業率で回帰するのをもう一度確かめてみよう。今回最新のデータまで含めてやり直してみたら次のようになった。
[回帰式C] 期間1954-2007、標本数54
log 犯罪率=0.369+0.837×log 前年の犯罪率+0.025×その年の失業率
重決定係数0.943、定数項のp値0.0035、log 前年の犯罪率の係数のp値4.6×10-22、失業率の係数のp値0.010。
とてもよい結果に見える。しかし誤差の系列相関の問題はどうだろうか。去年の「続報」記事にも書いたが、説明変数に被説明変数の過去の値が含まれるときには、ダービン・ワトソン値は使えない。この場合、「h統計量」というものが使われる。エクセルでは、さっき出てきたρ(今の場合は、0.543になった)と回帰分析結果の表を使って、次のように計算する。(「観測数」というのは標本数のことで、今の場合54)
=「ρのセル」*SQRT(「観測数」/(1-「観測数」*「被説明変数の前期値の係数の標準誤差」^2))
このh値は標準正規分布するそうで、大きいとダメということになっている。標準正規分布の2.5%水準点は1.96なので、hがこれより小さければ、(2.5%の2倍の)5%以上の確率でρ=0(系列相関なし)という仮説が受容されるということになる。
去年やったケースでは、2004年までの標本数51で、h=1.76となり、かろうじてこの基準では系列相関なしということが受け入れられた。もっともこれはかなり危ういところで、標準正規分布の5%水準点になると1.645なので、10%水準だったら系列相関なしの仮説は棄却されてしまうことになる。
では今回の、2007年までの3年分のデータを加えたケースではどうなっただろうか。実はh値は4.304ととても高い値になってしまった。この場合p値はほとんどゼロに近くなり、ρ=0(系列相関なし)という仮説は余裕で棄却されてしまう。
考えてみたらこの結果はおかしくない。上のグラフからもわかるように、90年代後半以降、犯罪率の失業率に対する反応は、それ以前と比べると早くなっている。新たに加えたデータも含むここ数年は、景気回復で失業率が減るのに合わせて、犯罪率も直ちに減り続けている。そうすると、計測期間全体から計算される予測値に比べて、現実の減り方の方が早くなる。よって、近年はマイナスの残差が続けて現れることになる。実際残差を見てみるとそうなっている。そのため、系列相関があるように計測されてしまうのだろう。
【これも2SPW法でやってみました】
とはいえ、本当に系列相関があるのかもしれないので、こっちも2SPW法でやってみた。すると、こんなふうになった。
[回帰式D] 期間1954-2007、標本数54
log 犯罪率を変換した変数=0.564×C+0.755×前年のlog 犯罪率を変換した変数+0.032×失業率を変換した変数
重決定係数0.999、Cの係数のp値0.004、前年のlog 犯罪率を変換した変数の係数のp値1.08×10-13、失業率を変換した変数の係数のp値0.009。
h統計量を計算すると0.669になる。上述の通り、標準正規分布の5%点は1.645なので、これ以上の系列相関なしという仮説は10%水準で余裕で受容される。
重決定係数はバカみたいに高いし、係数のp値も十分低いので、とりあえず、十分実証されたとみなしていいだろう。
【単位根と単純回帰の共和分】
ところで、私の大学院時代の計量経済学では習わなかったことだが、その後の計量経済学では、「単位根」とか「共和分」とかいうのを調べるのが主流になっているらしい。今までちょっと聞きかじっている限りではよく意味が分からなかったのだが、この際これもやってみないといけないだろうと、蓑谷本で勉強してみた。
付け焼き刃の理解だが、どうもこういうことらしい。「単位根」と「ランダムウォーク」とは違うらしいのだが、私にはよく違いが理解できないので、説明がごっちゃになってしまっているかもしれないが、今期の変数が、前期のその変数ずばりそのものに、出鱈目な変化が付け加わって決まっているとき、「単位根がある」と言うらしい。それで、変数Xと変数Yが、それぞれ無関係に、単位根があって出鱈目などこに行くかわからない運動をしているとき、見かけ上きれいに相関して見えることがあるそうである。だから、回帰分析をしてきれいな結果が出てもただちに信じるわけにはいかず、それぞれの変数に単位根がないか調べてみなければならないということらしい。
で、調べてみたらXもYも単位根がありましたということになったとしても、ただちに、残念でした無関係でしたねとはならない。両者の間に関係があってもそんなふうに観察される。しかし、本当に両者の間に決まった関係があって動いているのならば、Xの式から決まるYの予測値とYの現実値との残差は、プラス方向やマイナス方向でどんどん広がっていくことはない。残差の幅が大きくなれば、次期には縮小する方向に力が働くだろう。こういうのを「共和分」というらしい。もし、本当にXもYも無関係に動いているのならば、Xの式から決まる値とYの現実値との残差も、いくらでも勝手に拡大できるので、それ自体が単位根があるような出鱈目な動きをする。
で、今の場合についてこれを調べてみた。t期のXをXt、平均0散らばり具合一定で出鱈目に正規分布する項をεとすると、単位根があるというのは、Xt=Xt-1+εt、つまり、Xt=ρXt-1+εtのρ=1ということだから、この両辺からXt-1を引いて、Xの変化Xt−Xt-1をΔXtで表すと、
ΔXt=(ρ−1)Xt-1+εt
を(定数項0の)回帰分析にかけて、係数(ρ−1)がゼロとみなせるかどうかを確かめればよい。
「log 犯罪率」の場合、(ρ−1)は-0.00025と出たが、このt値は-0.104だった。回帰分析結果で表示されるp値というのは、このt値がt分布する場合の、この係数が本当は0である確率だが、単位根の場合、このt値はt分布しないらしい。だからここに表示されるp値を見るのではなくて、τ分布というのを調べなければならないらしい。蓑谷本500ページのτ分布表によれば、一番近い標本数50のときのτ分布の10%点は-1.61なので、t値はこれに比べて絶対値が小さすぎる。つまり、ρ=1で単位根があるという仮説は、10%水準で受容されてしまう。
失業率の場合は、(ρ−1)は約0.01。t値は0.747。標本数50のときのτ分布の90%点は0.91なので、やはりt値は小さすぎて、単位根があるという仮説は、10%水準で受容されてしまう。
ちなみに、変化分そのものに単位根があるかどうか、つまり、変数Xの場合、 Δ(ΔXt)=(ρ−1)ΔXt-1+εtの係数(ρ−1)がゼロとみなせるかどうかも調べてみたが、「log 犯罪率」の場合のt値は-3.41、失業率の場合のt値は-4.54となり、標本数50のときのτ分布の1%点は-2.62なので、いずれも単位根があるという仮説は棄却される。つまり、単位根がなくなる(「定常」と言うらしい)には、階差を一回とればよく、こういうのを「次数1の和分」と言うそうである。
それで、両方の変数とも和分の次数が同じなら共和分がとれるということなので、調べてみた。これは、まず犯罪率を失業率で普通に単純な回帰分析し、残差を出す。この残差をuとおくと、ut=ut-1+εt、つまり、ut=ρut-1+εtのρ=1だったら、やっぱり単位根があって共和分してないということになる。この場合も、この両辺からut-1を引いて、uの変化ut−ut-1をΔutで表すと、
Δut=(ρ−1)ut-1+εt
を(定数項0の)回帰分析にかけて、係数(ρ−1)がゼロとみなせるかどうかを確かめればよい。これって、伝統的計量経済学の誤差の系列相関のρが1かどうかということと同じことだという気がするけど、その場合はρは正規分布すると考えたのに対して、単位根のρは正規分布しないって考える違いがあるのかな。よくわからん。
とりあえず今の場合についてこれをやってみたら、係数(ρ−1)のt値は-1.649になった。
これを検定するには、MacKinnonの表とか言うものを使うらしく、これは蓑谷本では501ページに載っている。今の場合、変数が2で、No trend、10%点を見てみると、β∞=-3.0462、β1=-4.069、β2=-5.73となっている。これを使って、β∞+β1/標本数+β2/標本数2としたものが10%点の値で、今の場合では、-3.0462-4.069/54-5.73/(54^2)=-3.124になる。t値はこれよりずっと小さいので、ρ=1で単位根があるという仮説は、10%水準で受容されてしまう。うーむ。やっぱりうまくいきませんね。
【[回帰式C][回帰式B]の共和分】
そこで今度は、前年のlog 犯罪率を説明変数に入れた[回帰式C]の共和分検定を試みる。
[回帰式C]の場合は、よくわからないのだが、単純なやりかたではダメで、「log 犯罪率」が落ち着く長期の関係式を出さなければならないらしい。蓑谷本で438ページから書いてある。
[回帰式C]の「log 犯罪率」が右辺のも左辺のも同じ値をとると、右辺の「log 犯罪率」の項を左辺に移項して整理すると、
log 犯罪率=0.369/(1-0.837)+[0.025/(1-0.837)]×失業率
=2.253+0.153×失業率
という関係式になる。実際の「log 犯罪率」と、この右辺の値との残差をとって、あとはさっきと同じく、この残差の増分を前年の残差で、定数項なしの回帰分析にかけて、係数がゼロとみなせるかどうかを検討してみればよい。そうすると、係数のt値は-1.58になった。
501ページの表で変数が2で、No trend、10%点を見て、標本数54をあてはめて計算すると、さっきの場合と全く同じなので、-3.124になる。t値はさっきのケースよりもっと足りない。単位根があるという仮説は、10%水準で受容されてしまう。
ところで、さっきやった2SPW変換した式は、共和分という考えになじむのかなじまないのか私にはさっぱりわからないのだが、とりあえずやってみた。
すなわち、[回帰式B]の残差を使って、残差の増分を前年の残差で定数項なしの回帰分析にかけたら、係数のt値は-4.376になった。この場合、変数は、定数項を変換したものも含めて数えるのかどうかわからないのだが、得たい結果にとって厳しい方をとって、それも含む変数の数3で調べることにする。すると、変数の数3、No trend、標本数54のときの5%点は、-3.7429-8.352/54-13.41/(54^2)=-3.902になる。この場合めでたく棄却域に落ちて、共和分しているということになる。
もっとも1%点になると、-4.569でわずかに及ばない。だが変数の数2のときの1%点になると、-4.105なのでクリアしている。
とりあえず、[回帰式B]の場合は、5%水準では十分単位根が棄却され、共和分していると認められるようである。
まあ、本を見ながらの見よう見まねで、自信はないから、この結果を無批判に引用したりはしないでほしい。よくわかっていない身のフィーリングで言えば、どうもこの「単位根」とか「共和分」とかの考え方だけど、経済を実証するのに、消費関数とか投資関数とかみたいに、ある期間の中で内生的に決まる変数を使って計量分析するのをやめてしまって、時間を通じて変化する変数間の動学的な運動方程式に全部落とし込んでから計量にかけるのが流行りになっているようで、そういう変数の自己運動みたいな見方で全経済を見るときに必要になる考え方のような気がする。だから、今のケースのように、特定の二変数間の関係に絞り込んだ命題の実証にそぐうものなのかどうかということはよくわからない。とっても気持ち悪いのだが、その気持ち悪さを論理的に説明する能力は何もないので、とりあえずみんながやってそうなことはやりましたということで、あとは専門家が詰めてくれることに期待したい。
【殺人と失業再び】
さて、去年の「続報」記事では、上記のような犯罪と失業率の関係は、ほとんどが窃盗の動きであろうということを指摘し、ではもっと重い犯罪ではどうなるのかということで、殺人と失業の関係も検討した。そこに載せたグラフを再掲するとこんなのだった。
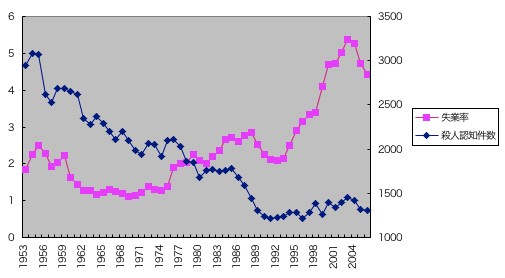
つまり、殺人認知件数は、長期的に低下するトレンドがあり、そのトレンドを除く細かな上下は、やはり失業率が影響していそうなのである。
このトレンドは、一人当たり所得によるものかもしれないし、少子化によるものかもしれないし、高齢化によるものかもしれないし、長期トレンドを持つ要因はいくらでも思いつくから、どれだということを決めつけることは不可能だと思うが、とりあえず一番簡単に、単純な時間トレンドで調べてみたのだった。
そうすると、去年の記事では、殺人認知件数を直接に失業率と年次で回帰分析したら、一見非常に実証結果がよかったけど、実はダービン・ワトソン値が低くて、誤差の系列相関が観測されてしまった。しかし、この同じ式の階差をとって、殺人認知件数の変化を失業率の変化で回帰分析したら、誤差の系列相関は全くなく、決定係数は低いが定数項と係数は有意に観測された。この定数項は時間トレンドを表しているので、時間を通じて減少する傾向があると同時に、失業率が増えると殺人件数も増えるという関係が実証されたわけである。
今回もこれをまた確認してみたい。
「殺人認知件数」は上記の統計局の犯罪データのファイルの「G列」にある。05年以降のデータはさっきの警察庁のファイルの「A-a」シートから継ぎ足せはよい。
本当は殺人認知件数も人口が増えれば増えると思うので、人口で割って、人口百万人あたりの殺人認知件数にしておく。これを以下では「殺人率」と呼ぶことにする。
それで、「殺人率」を年次(西暦)と失業率で回帰分析したら次のようになった。
[回帰式E] 期間1953-2007、標本数55
殺人率=1199.04−0.600×年次+2.862×失業率
重決定係数0.969、定数項のp値5.44×10-37、年次の係数(トレンド)のp値1.63×10-36、失業率の係数のp値4.83×10-16、ダービン・ワトソン値0.661。
やはり、一見非常に成績がよいが、誤差の系列相関があるので認められない。
【系列相関を除去する実証分析】
この問題に対処するために、まず去年と同じく、[回帰式E]の両辺から一年前にずらした同じ式を引いて、殺人率の階差と失業率の階差の回帰分析をやってみる。するとこうなった。
[回帰式F] 期間1954-2007、標本数54
殺人率の階差=−0.518+1.494×失業率の階差
重決定係数0.133、定数項(トレンド)のp値0.0005、失業率の係数のp値0.0067、ダービン・ワトソン値2.088。
やはり去年と同様、ダービン・ワトソン値はとても改善され、誤差の系列相関はなくなった。定数項も係数もp値がとても低く、統計的に有意であることが認められる。ただし、重決定係数は低いので、減少トレンドや失業率の影響はあるのは事実だが、でてきた数値自体は信用できない。実際、[回帰式E]と比べてみると、トレンドや失業率の係数の数値はかなり食い違っていて安定していない。
そこでまたここでも2SPW法をやってみることにする。年次トレンドがあるものにこんな手法が使えるのかどうか心もとないのだが、そこはしろうとの強みで目をつぶって、年次も一つの普通の説明変数とみなしてやってみた。その結果はこうなった。ただし、ρ=0.572となる。
[回帰式G] 期間1953-2007、標本数55
殺人率を変換した変数=1154.54×C−0.577×年次を変換した変数+2.525×失業率を変換した変数
重決定係数0.986、Cの係数のp値3.11×10-27、年次を変換した変数の係数のp値8.77×10-27、失業率を変換した変数の係数のp値1.01×10-8、ダービン・ワトソン値は1.460。
これも非常に良好な実証結果に見えるが、ダービン・ワトソン値は微妙である。そこで表を調べてみた。すると、説明変数3、標本数55の1%点のdL=1.284、dU=1.506なので、この結果はこの間に入る。つまり、ρ=0は1%で棄却も受容もされない。誤差の系列相関はあるともないとも言えないという結果になった。
【単位根と共和分の検定】
そこでまた、単位根と共和分の検定をしてみることにした。
まず、殺人率だが、これは明らかに減少トレンドがあるので、これまでと同様に、「殺人率階差=δ×前年殺人率+ε」という形で回帰分析にかけると、係数がマイナスに出るのは当然である。実際、係数のt値は-3.98になり、これは単位根存在の仮説を棄却させる。しかし、この場合には、「殺人率階差=μ+δ前年殺人率+ε」と、定数項がある形で調べるべきだろう。そうすると、単位根がある仮説は受容されることになる。ただし、この回帰分析結果では、定数項はマイナスになるべきところ、プラスで出てしまっているが...。
それで、年次トレンドを入れた関係式の共和分なんてどうやって調べるのかわからないのだが、とりあえず年次もただの普通の変数とみなして[回帰式E]の関係式でやってみると、残差の係数のt値は、-2.889となった。これは、MacKinnonの表のどこを見ればいいのか、「With trend」というところを見るべきような気もするが、ここで言う「trend」というのは残差のトレンドだから「No trend」でいいような気もしてよくわからないのだが、どっちにしろこのt値の絶対値は小さすぎて、単位根がある仮説は受容されてしまう。
それでまあ、[回帰式G]の関係式でも共和分検定をやってみた。まあこんな2SPW変換したもので、しかも年次トレンドのあるものでこんなことができるのか、できたとして普通のやりかたのままやっていいのか疑問はいくらでもあるのだが、そこはまたしろうとの強みで目をつぶってやってみたら、係数のt値は、-5.836になった。
これも変数の数が3なのか4なのか、「No trend」を見ればよいのか「With trend」を見ればよいのかわからないのだが、変数の数が3より4の方が、「No trend」よりも「With trend」の方が、こっちにとっては都合が悪いので、一番都合が悪い変数4、「With trend」で見ると、1%点は-5.403になる。係数のt値は絶対値がこれより大きいので、棄却域に落ちて、共和分していると認められる。変数が3になったり、「No trend」になったりすると、1%点の絶対値はもっと小さくなるので、なおさらこの結論は言える。
まあそういうわけで、去年の記事の結論は、やっぱり言えるんじゃないでしょうかというのが今回の結論です。自分では学術的に発表するつもりはないので、計量の専門家か専門を志す人の誰かが詳しい研究をやってくれることを期待しています。
「エッセー」目次へ
ホームページへもどる

