松尾匡のページ10年2月20日 四年生ゼミ生の実証分析続報
大学院の入試業務で昨日から立命館にきているところです。
昨日『図解雑学』の見本原稿をやっと送ったところ。2月のはじめに督促メールを受けてあせっていたのですが、編集者様からはお誉めの言葉をいただき一安心です。「少し急いでいただくと幸い」とのご指示もいただいたので、あんまりゆっくりもしていられないのですけど...。
で、前々回のエッセーに引き続き、久留米大学の四年生の論文の中身の紹介なのですけど。
まず、ブレーク・イーブン・インフレ率で回帰分析してくれたA君の研究。
ブレーク・イーブン・インフレ率って、このエッセーでも何度か触れてきたのですが、普通の国債の利回りから物価連動国債の利回りを引いたものです。どちらを買っても収益がトントンになるように市場で裁定が働きますので、この率は、市場参加者の頭の中にある将来のインフレ予想を表しています。実際には、いろいろなバイアスがあるのではないかと指摘されているのですが、まあひとつの目安としては役立つだろうということです。
これ、日々の「セコハン」市場で決まる利回りから計算されるやつは、財務省のサイトの次の場所にグラフが載っています。
http://www.mof.go.jp/jouhou/kokusai/bukkarendou/bei.pdf
財務省サイトのトップから行くには、「トップ > 国債等 > 入札関係 > 物価連動国債 >ブレーク・イーブン・インフレ率の推移」と進んで下さい。
しかし、これの元になっている日々の「セコハン」市場の利回りのデータそのものは、ウェブ上で取れるものが見つかっていません。
A君がやってくれたのは、財務省サイトで「トップ > 国債 > 国債関係諸資料」と行くと、過去の国債入札の結果がエクセルで取れますので、ここに出ている、10年物国債と10年物(しかないが)物価連動国債との、近接した入札日のものの入札時点の最高利回りの差を出すというものです。
それは、こんなふうになりました。
| 04年3月 | 0.061% |
| 04年6 | 0.413 |
| 04年12 | 0.868 |
| 05年6 | 0.638 |
| 05年9 | 0.466 |
| 05年12 | 0.563 |
| 06年3 | 0.826 |
| 06年6 | 0.855 |
| 06年8 | 0.948 |
| 06年10 | 0.619 |
| 06年12 | 0.476 |
| 07年2 | 0.424 |
| 07年3 | 0.388 |
| 07年6 | 0.530 |
| 07年8 | 0.553 |
| 07年10 | 0.345 |
| 07年12 | 0.259 |
| 08年2 | 0.305 |
| 08年4 | -0.050 |
| 08年6 | 0.423 |
| 08年8 | 0.324 |
それで、これとか、あと日銀のホームページに出ているプライムレートからこれを引いて出した「実質利子率」とかを、月次データが出ているいろんな景気関連の統計と比較して、かたっぱしから回帰分析していったんですわ。こんなことするのは学生ならではの力技ですが。
そしたら一番よかったのが、1年後の東証株価指数の前年同月比。まあ要するに、その時点から1年後までに株価が何パーセント変化したかということです。お互いの推移のグラフはこんなの。
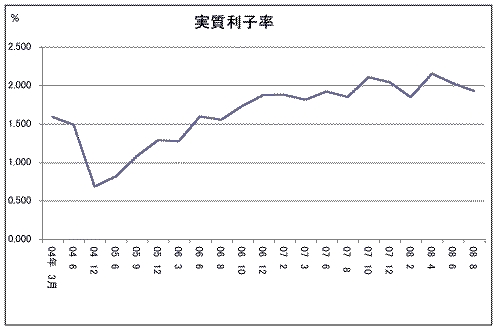
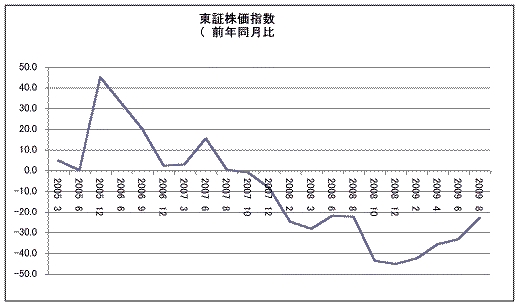
一応彼が出した回帰分析結果は、次の通りでした。
観測数21
1年後の株価上昇率(%)=82.98−56.48×実質利子率(%)
重相関係数0.918(重決定係数0.842)、切片のp値は小数点以下8桁のオーダーの微小値、係数のp値も小数点以下9桁のオーダーの微小値になりました。散布図はこんなの。

まあ、この限りではとてもいい結果ですけど。しかし、リーマンショック後の株価の変動が推計期間に含まれていて、こんなのが1年前から決まっていたとはとても思えないから、実はだいぶ怪しい結果ではありますな。リーマンショック後のデータを除いても結果が悪くなるとは思えませんが、今度はサンプル数が少なくなるのであまり統計的意味はなくなる気がします。ただの偶然の可能性も高いですよーということはとりあえず言っておきます。
理論的にも、株価が株と債券の代替で決まるとすると、実質ではなくて、名目利子率の方とマイナス相関するはずですね。因果関係があるとすると、実質利子率が設備投資に効いて、それが総需要に影響して、1年先までの株価を動かすという関係でしょう。だから本当は設備投資との関係を調べるのがいいのでしょうけど、設備投資統計は四半期データしかないので、今のところは時点がズレたり、サンプルが少なかったりして無理です。
もちろん学生の論文では誇らしげに掲げられた結果になっていることは、暖かく受け止めていただければ幸い。
ところでこれ、データが不定期なので、誤差の系列相関とか調べるの意味ないのですけど、機械的にダービン・ワトソン値を出したのでは、系列相関がないことになっています。
それでボクはこれを見て、これがもしホントだったらアメリカのデータで同じことが実証できるはずだと思いました。アメリカだったら、2003年から物価連動国債の利回りの月次データがある(普通の国債の利回りの月次データはもっと前からある)ので。でも実際やってみると、むしろプラスに効きます。これは、たぶんアメリカの場合、株価の動きを見て、機敏に金融政策が動いているからだと思います。
だから、名目利子率は除いて、株価とブレーク・イーブン・インフレ率そのものとの関係を見た方がいいです。すると4ヶ月ほどのラグでいい相関をします(株価の方が遅れる)。これは、因果関係というよりはむしろ、共通の将来予想を反映しているのだと思います。
次に、アメリカの投資関数の実証をしてくれたK君の研究。
実は彼は、三年生のときの論文で、いろいろな国のいろいろな時代のGDP成長率とか、GDPのトレンドからの乖離とかを、スペクトル分析にかけたのでした。スペクトル分析というのは、変動するデータの動きを、いろいろな波長の波の合成ととらえて、いろいろな周期の波に分解することです。
その昔、景気の波には、3〜4年周期の波の他に、10年前後周期のジュグラーの波とか、30年位の周期のクズネッツの波とか、50年周期のコンドラチェフの波とかがあると言われていたのですが、今の主流学説では、目の前に見える3〜4年周期の波だけがあって、しかもそれは決まった周期性があるものではなくて、それを超える周期の波なんてトンデモ論だということになっていると思います。
しかし、三年生のときのK君の論文では、目の前の3〜4年周期よりも長い、必ずしも10年とは言えないけど、何か16年周期(2のベキ乗数の周期しか出せないのでこうなる)ぐらいの波が検出されるケースが多いことは否定できないという結果になりました。
そこで今回彼は、設備投資に効く長周期の要因を探ろうとしたわけです。
このサイトの「アカデミック小品」のコーナーに、以前ボクが作った資本ストックの平均年齢を簡易計算するエクセルファイルがあります。各年の資本ストックと設備投資のデータをコピーペーストすると、各年の資本ストックの平均年齢が出てくるというものです。
K君はまず、アメリカのデータでこれをあてはめて、資本ストックの平均年齢を出しました。いろいろ試したのですが、結局、製造業で、しかも、建物が入ると年齢が高くなってずいぶん周期が伸びるので、IT以外の機械・設備のデータを使うことにしました。
この資本ストック平均年齢と、各年の資本ストックに対する設備投資の比率をグラフにして推移をみると次のようになります。
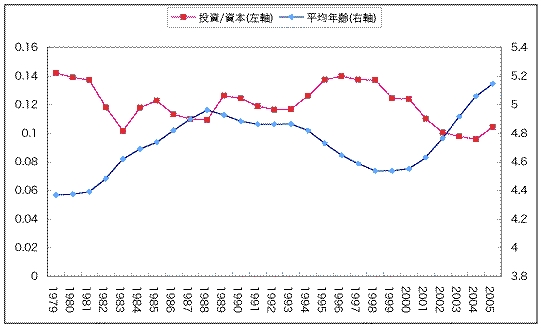
だいたい逆の動きをしているように見えますので、とりあえず回帰分析すると、重相関係数0.647(重決定係数0.419)で、係数のp値は0.00026と、それなりにいい結果がでました。それで、これ以外の要因を調べるために、プライムレートを名目利子率と考えて、今の回帰分析の残差と重ねてグラフにすると、次のようになります。
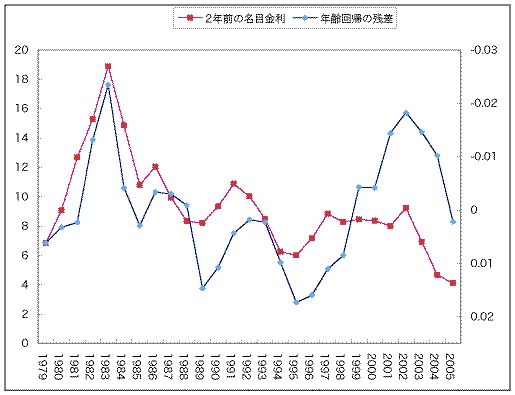
ただし、名目利子率は2年のラグをつけています。また、資本ストックでの回帰の残差は、見易いように、右軸目盛りの上下を逆転させています(上に行くほど小さくなる)。
動きがよく似ていますので、K君は、資本ストックに対する設備投資の比率を、資本ストック平均年齢と名目利子率の二つで回帰分析しました。その結果はこのようになりました。
観測数27
設備投資/資本ストック=0.382−0.052×資本ストック年齢−0.0016×名目利子率(%)
重相関係数は0.737(重決定係数は0.543)、切片と第1説明変数の係数、第2説明変数の係数のp値はそれぞれ、小数点以下8桁のオーダー、小数点以下5桁のオーダー、0.0177となりました。
まあ、わりといい結果と言えると思います。もっとも、実はダービンワトソン値はだいぶ低くて、誤差の系列相関があると言えます。よく考えたらそれもある意味当然で、資本ストック平均年齢というのは、資本ストックに占める過去の設備投資の比率をウェートにして計算しているわけですから、ラグ付きの自己回帰をやっているのと似たことになるのですね。まあ学生の論文ではこんなことは触れてませんけど、これも暖かく受け止めていただければ幸い。
それで、彼は、名目利子率の係数のp値が1%より少し大きくなってしまったので、実質利子率でやろうとしました。でもブレーク・イーブン・インフレ率は2003年からしかありません。仕方ないので、名目金利時点のGDPデフレーターの対前年変化率や、その前年のGDPデフレーター対前年変化率をインフレ予想の替わりに使って実質利子率を出してやってみたのですが、いずれも、若干ですが回帰分析の実証結果は名目利子率を使った場合よりもかえって悪くなります。
残念ながらここで時間切れになっているのですけど、ボクの予想では、この設備投資は製造業だけのものなのに対して、GDPデフレーターが示す物価は、GDPを構成するすべての財・サービスの価格が含まれてしまっているのがうまくいかなかった原因ではないかと思います。製造業製品の価格上昇率は、物価一般の上昇率よりも、1990年代後半以降はかなり低くなっているはずなので、これだけを取り出して名目利子率から引いて実質利子率にすれば、90年代後半以降の山がもっと高くなって、設備投資比率の減少をよく説明できるのではないかと思います。
まあとりあえず、設備投資の長期的な変動が、資本ストックの平均年齢が高まったら増え、若くなったら減ることで説明され、短期的な変動は金融的要因で左右されるというのは、まあわりと理にかなっているのではないかと思っています。
さて、K君の回帰分析でも2年のラグが出てきましたし、上のボクがちょっとやってみたアメリカの株価の話についても4ヶ月のラグが出てきましたが、どうやって当たりをつけたと思いますか。
学部学生にアーモンラグなんてやらそうなんて無謀もいいとこなので、もちろんそんなことはしません。
ヒトから聞いたアンチョコの当たりのつけかたを使っているのです。エクセルでちょこちょこっとできるので、いいかげんなんですが便利なのでここでオープンにしておきます。もうみなさん周知のことかもしれないので、もしそうなら恥ずかしいのですが、グーグルで探してみたけどどこにも説明してないみたいなので。
例えばA列に説明変数、B列に被説明変数の時系列データを1行から100行までとっているとき、10期のラグまで確かめたい時には、C1セルに、
=CORREL(A$1:A$90,B1:B90)
として、これをコピーしてC2からC10までペーストすればいいのです。出てきた数値が一番大きいズレ方をラグに使うというわけです。厳密には使っているデータが違うので相関係数を比べていることにはならないのですが、期間が長ければ当たりをつけるぐらいはできるというわけです。最初教えてもらったときは驚愕したわ。
「エッセー」目次へホームページへもどる




